Home -> Ptolemaic
System ->Notable Features
Ptolemaic Astronomy
Astronomy is the oldest as well as the most prestigious of the mathematical sciences.
Observing the heavens for the purposes of predicting eclipses and other phenomena occurred
in the time of the Babylonians, if not earlier. Well before the beginning of the Christian
era, astronomy was a demanding technical enterprise. It required long training and intense
dedication of its practitioners. In this module, the computer will stand in for that
training, and provide you with the theoretical toolkit possessed by a practitioner of
Ptolemaic astronomy.
For much of its history, planetary astronomy, at least, has been dominated by a
relatively simple set of conceptual tools. Any late-medieval or Renaissance astronomer was
familiar with these tools. This module recreates the practice of astronomical theorizing
pursued by such an astronomer.
What does an astronomer do, and why does he or she do it? In this period, an
astronomer's duty was to predict planetary positions and eclipses. To achieve those ends,
he might have to construct both observational instruments and theoretical constructs. By
contrast, there were some surprising things that an astronomer did not do. He did
not concern himself with the nature of the heavens and heavenly bodies themselves - at
anything beyond a fairly elementary level, at least. He was regarded as unqualified to
speculate extensively on the causes of celestial motions, nor, indeed, to probe far beyond
the numerical figures themselves that he derived from observed planetary positions. And he
was not very concerned, even within this calculational work, about the actual paths
followed by the planets through the heavens. These were matters on which the mathematical
techniques of astronomy could yield no certain or authoritative knowledge. They were more
appropriate to the philosopher than the mathematician, since they related to real,
physical entities, not abstracted, numerical ones. An astronomer was correspondingly
something of a subordinate figure. His was a service industry, dedicated to providing
dates and times for others of higher status (physicians, churchmen, philosophers) to put
to use.
Ptolemaic astronomers thus avoided controversial speculation on the nature and
mechanisms of the heavens. But their basic assumptions were nonetheless supposed to be
compatible with natural philosophy -- and in particular the natural philosophy of
Aristotle.
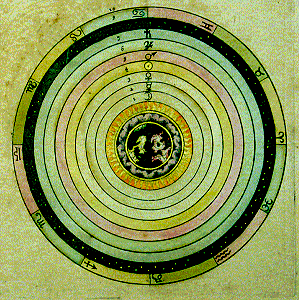 |
As seen here in a hand-colored image from a seventeenth-century atlas,
Aristotelian natural philosophy portrayed a cosmos with the Earth stationary at its
center. The four elements of earth, water, air, and fire all had their own proper spheres
concentric to the earth, followed by the sphere of the Moon. This marked the boundary
between the "sublunary" world, in which things came into being, changed, and
died, and the "superlunary" realm, in which things were eternal. Beyond lay the
planets, or "wandering stars," which moved around the earth in perfect spheres.
The sphere of the fixed stars contained all of these, with nothing beyond it except God.
Christians changed the gloss slightly to assert that the cosmos as a whole was not eternal
- it had been created by God, they insisted, and would eventually suffer annihilation at
his hand - but they kept the natural-philosophical principles largely intact. On this
basis, Christianized Aristotelianism provided coherent and largely convincing knowledge of
natural processes for some 450 years, from the reintroduction of Greek philosophy in
around 1200 to its eclipse in the "Scientific Revolution" around 1600-1650. |
But astronomers were not philosophers. They accepted the basic structure of the
Aristotelian cosmos, but did not see their task as one of explaining its nature. Their
role was to predict significant celestial events (like eclipses and conjunctions ),
provide astrological forecasts, and identify propitious days on which to administer
medicines. For such purposes Aristotelian cosmology proved not so much inadequate as
inappropriate. Astronomers instead developed their own, rich, mathematical tradition. But
the result was a multiplicity of different theories, all unique, but all properly called
"Ptolemaic" because they embodied the theoretical devices of the Almagest.
What was it like to pursue this kind of enterprise - an enterprise very different
from the modern science of astronomy, and yet of which that modern science is
the descendant? In this module you are given the chance to find out. You yourself
become a Ptolemaic astronomer. The computer provides you with the theoretical
armoury an astronomer possessed as a result of his training at university
or through dedicated reading. You are faced with an observed path of a planet.
Your task is effectively that faced by any astronomer of the Middle Ages or
Renaissance seeking to placate his prince or advance in his university. Can
you achieve success?
Click here for detailed instructions, or begin
the Simulation
Ptolemaic Astronomy: Some Conclusions
You have probably left the simulation with your theoretical model matching the observed
motions well in some places, but with distressing divergences in others. In that, your
experience has corresponded fairly well to those of Ptolemaic astronomers in medieval
Islam and Renaissance Europe. Exercising the kinds of judgment they exercised should also
have served to fix in your mind some characteristics of astronomy as it was then defined
that may seem puzzling to a modern user. And it may well have raised questions that would
not have occurred to a real Ptolemaic astronomer at all. These questions reach to the very
definition of astronomy - and they profoundly affect how we think of its history.
Theory Construction: Is Empiricism Enough
One of the most difficult practical questions for an astronomer doing this kind of work
was this: when do I stop? By combining equant, deferent, and epicycle, you will be able to
match the motions of a planet fairly closely. But how closely is sufficient? And how do
you know that the degree of approximation you choose is the right one? Bear in mind that
much may hang on your decision, from the date of Easter to the moment when you take your
medicine. In fact, the decision to stop doing astronomy marked the moment when a
new theory came into being.
But this was not the end of the problem. Not only was the appropriate degree of
exactitude obscure; there were also an indefinite number of ways of achieving it. With
Ptolemaic assumptions and tools, an astronomer could "save" the appearances of a
planet in an infinite number of ways. Who was to decide which of these ways should be
preferred, and be accounted an astronomical theory? On what grounds?
It is particularly evident, then, that given a practice of this kind, the knowledge
that Ptolemaic astronomers prized as their achievement was of a peculiar sort by the
lights of modern science. It could be very precise, and accurate to the nth
degree, and there was widespread agreement about the legitimacy of Ptolemaic assumptions
in general - yet there was no guarantee as to the physical truth of any theory in
particular. This reflects very important characteristcs about both the natural world of
the Renaissance and the social world of the astronomers.
In the sixteenth century awareness of such conundrums gave rise to fierce controversy. Nicolaus Copernicus wrote De Revolutionibus
(On the Revolutions) out of conviction not only that the earth was in motion, but
that certain knowledge of astronomical motions was possible.
What is an Orbit
Ptolemaic astronomy could produce a planetary trace matching observations in any number
of ways. But the theories might not be equivalent after all. The actual paths followed
through space by the planets carried on all those epicycles and deferents differed widely.
Some of these planets had orbits so bizarre that they could not really be accounted orbits
at all. Could this not provide grounds for choosing between rival proposals?
In practice, it often could not. The reason for this lies in what Ptolemaic astronomers
knew about both the physical and the social worlds.
It seems obvious today that mathematics has a principal part to play in understanding
natural phenomena. But in Renaissance Europe this was widely doubted. Aristotelian
philosophers in particular tended to regard the making of claims about nature on the basis
of mathematical arguments with suspicion. It seemed to them to embody a fundamental
category mistake. The point of natural philosophy was to consider nature in its
substantial whole, and to provide causal accounts of why phenomena occurred as
they did; mathematics treated quantity - at best but one aspect of such phenomena - and
had nothing to say on the crucial matter of causation. The mathematical sciences were
therefore "mixed," in that they applied mathematical techniques to
inappropriate, non-mathematical objects. They might produce tangible effects, but not real
philosophical knowledge.
Most Ptolemaic astronomers would have agreed. Theirs was a mathematical enterprise.
That is, it did not advance philosophical claims about the nature of the heavens, the
heavenly bodies, and their motions. It was not that they did not see the value of seeking
the truth about such matters; solely that mathematics was not the enterprise for those
doing so. The right enterprise for such seekers was natural philosophy. Natural
philosophers were thus more prestigious than astronomers (and all other mathematicians).
They received greater salaries and more renown.
Finding out about Ptolemaic practice thus not only reveals important information
about astronomy - showing what a different enterprise it was in the Renaissance
from the science that now goes by the same name. It also tells us something
important about the natural philosopher's role, too. And it shows how those
two distinct disciplines resulted in the nonexistence of something that to us
seems a self-evident presence in the world. In fact, it is not just that the
more crazy planetary paths generated by Ptolemaic mechanisms cannot be accounted
orbits. None of the paths are orbits. Even when Copernicus published his De
Revolutionibus, working astronomers could comfortably transform his models
into a system with a stationary Earth because for someone pursuing this practice
the reality of these paths required no commitment. Only when Johannes Kepler
overthrew the entire practical enterprise of Ptolemaic astronomy did the concept
of an orbit begin to have some meaning. Yet even Kepler owed something to Ptolemy.
He rejected existing astronomical theories - and the entire enterprise of which
they were the product - partly by reviving a very ancient idea that the universe
must exhibit harmony, and by insisting that it was his role to understand
this harmony. And Kepler was convinced that Ptolemy had known this long before
him. He tried hard to recover and complete a long-neglected text by the ancient
astronomer on the subject of harmony itself
- a text which, he believed, would reveal the commitment of Ptolemy to identifiably
similar views. The ravages both of time and of the religious wars of Kepler's
own age foiled this plan to revive Ptolemy for yet another age.
Site Map | Contact Us
